Excelのデータ列の中で、値の大きい順または小さい順に順位付けをしたい場合はRANK関数を使います。
データ値を対象にして各行を比較するときには、並べ替えやオートフィルターを使うことが多いのですが、RANK関数を使えば並び順はそのままの状態で、順位を表示させることができます。
この記事では、ExcelのRANK関数を使ってデータ値の大きい順、または小さい順に順位付けをする方法を紹介します。
RANK関数で順位を付ける
早速、RANK関数の使い方を見ていきましょう。その前に、RANK関数にはいくつかの種類があります。
まずは、それぞれのRANK関数について説明します。
[RANK]と[RANK.EQ]と[RANK.AVG]
Excel上でデータ値の順位を求めるときに使われるRANK関数には、[RANK]と[RANK.EQ]と[RANK.AVG]の3種類があります。
RANK関数
最もシンプルな名称のRANK関数は、実は古い型の関数です。Excel2010以降は後述する[RANK.EQ]と[RANK.AVG]に細分化されました。
当記事執筆時点で、RANK関数はまだ使うことができますが、今後のバージョンアップのため、今から使うのであれば[RANK.EQ]または[RANK.AVG]を使うようにしましょう。
RANK.EQ関数とRANK.AVG関数
RANK.EQ関数は、前述した通り、2010以降の新しい関数名です。働きは従来の[RANK]関数とまったく一緒です。
RANK関数が、[RANK.EQ]と[RANK.AVG]に細分化された理由は、順位付けをするうえで、同順位が発生した場合の表示方法を選択可能にするためです。
一般的に、スコア等の順位付けをする際に同順位が発生した場合には、次の順位を繰り下げて表記しますが、今回の両関数ではその表記方法が異なります。
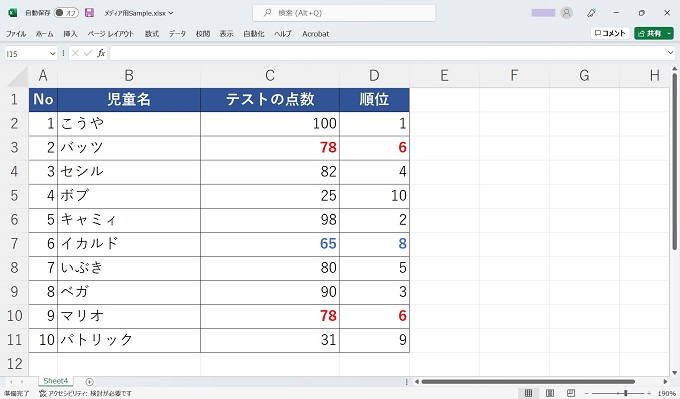
RANK.EQの表示
RANK.AVGの表示
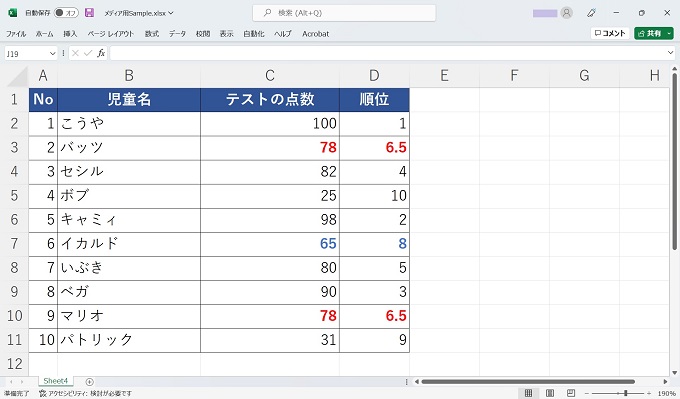
上記はある小学校で実施した児童のテストの点数を記録したExcelシートです。[No2.バッツ]と[No9.マリオ]が78点で同順位となっていますが、RANK.EQの場合は6として表示しているのに対して、RANK.AVGでは6.5と表示されています。
両関数の違いはこの点でだけとなりますので、一般的な表示でよければ[RANK.EQ]を使えば問題ありません。
RANK(EQ.AVG)関数の使い方
数式
=RANK.EQ(数値,データ範囲,順位)
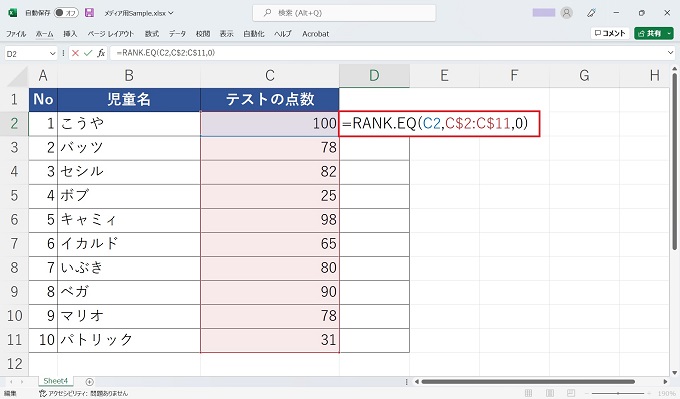
例:=RANK.EQ(C2,C$2:C$11,0)
上記がRANK.EQ関数の使い方です。なお、RANK.AVGを使う場合には、[EQ]の箇所を[AVG]に書き換えるだけで、以降の構文は一緒です。
重要な点として、上記数式の「数値」はランク付けをする対象の数値になりますので、相対参照で記述する必要があります。(例_C2)
「データ範囲」については、ランク付けをするためのデータの母集団になりますので、絶対参照で記述します。(例_C$2:C$11)
そして、順位については、降順(大きい順)なら0を、昇順(小さい順)なら1を指定します。なお、デフォルトは降順のため、0であれば省略することが可能です。
RANK(EQ.AVG)関数の実例
下記はある小学校で実施したテストの結果を管理しているExcelシートです。当記事では、このExcelシートをサンプルにRANK関数を使って順位付けをしてみます。
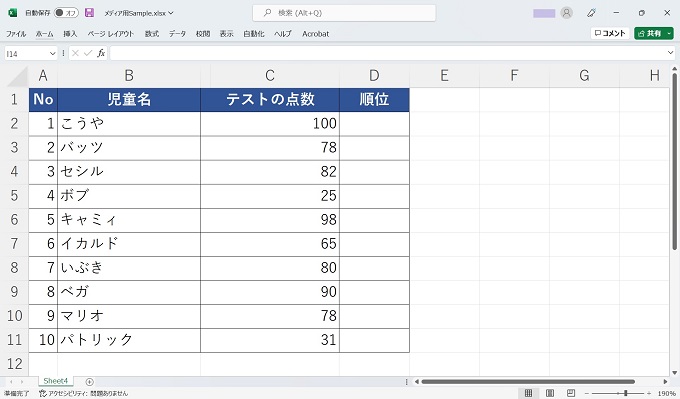
手順
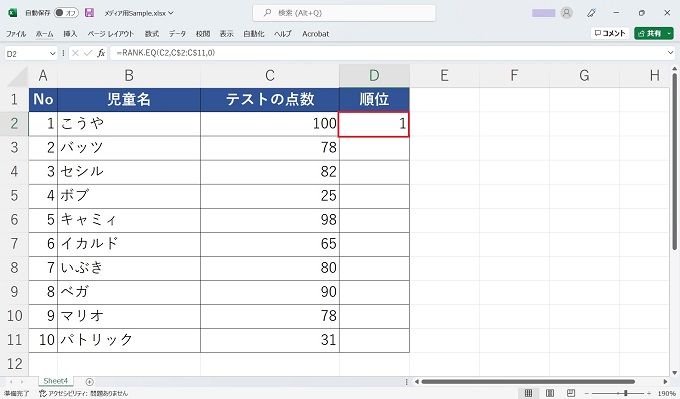
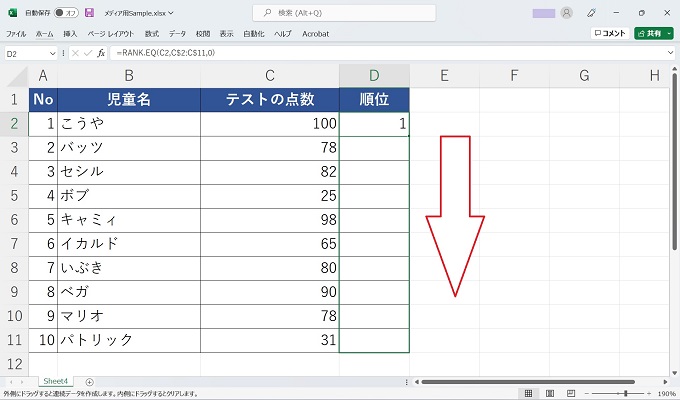
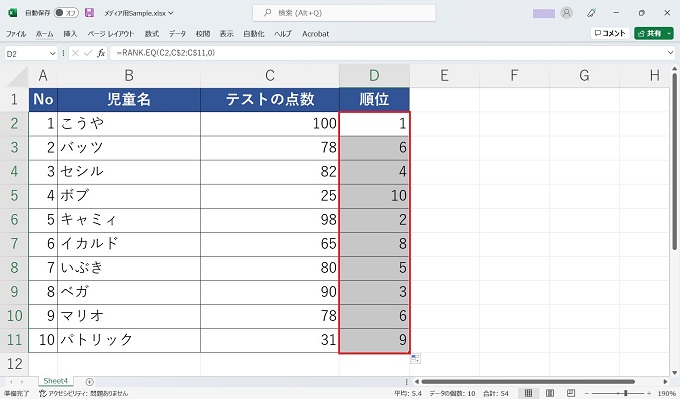
あとがき
今回は、ExcelのRANK関数を使ったデータ列の順位付けについて記事にしました。
順位付けは、データ分析を行ううえでもよく使う機能のひとつです。たとえば、ベスト3やベスト5などを抽出するときにも便利に使えると思います。
特に、実務で使用する売上金額等の場合には、数値が大きくなりますので、RANK関数を使った順位のほうが一見して分かりやすいといった利点もあります。
ぜひ活用してみましょう。
